Exploratory analysis

Model-based Geostatistics for Global Public Health

Author
Affiliation

Emanuele Giorgi

Lancaster University

Overview of topics

  • How to explore relationships with count data
  • How to use a non-spatial model for mapping
  • How to handle spatial data in R

Example: Riverblindness in Liberia

  • How to explore relationships with count data (binary and aggregated counts)?
  • How to model non-linear relationships?
  • How to assess residual spatial correlation?

explore_associations.R

Overdispersion in Count Data

  • What is overdispersion?
    • Occurs when the variance of count data exceeds the mean.
    • Violates the Poisson assumption:
      \[ \text{Var}(Y) = \mathbb{E}(Y). \]
  • Why does it matter?
    • Standard models (e.g., Poisson regression) underestimate uncertainty.
    • Leads to overly optimistic confidence intervals and p-values.

Example: Overdispersion in Correlated Binary Data

  • Consider \(Y = \sum_{i=1}^n X_i\), where \(X_i\) are correlated binary variables.

. . .

  • If \(X_i\) are independent, \(Y\) follows a Binomial distribution: \[ \mathbb{E}(Y) = np, \quad \text{Var}(Y) = np(1-p). \]

. . .

  • If \(X_i\) are correlated, the variance increases:
    \[ \text{Var}(Y) = np(1-p) + \sum_{i \neq j} \text{Cov}(X_i, X_j). \]

. . .

  • This leads to overdispersion.

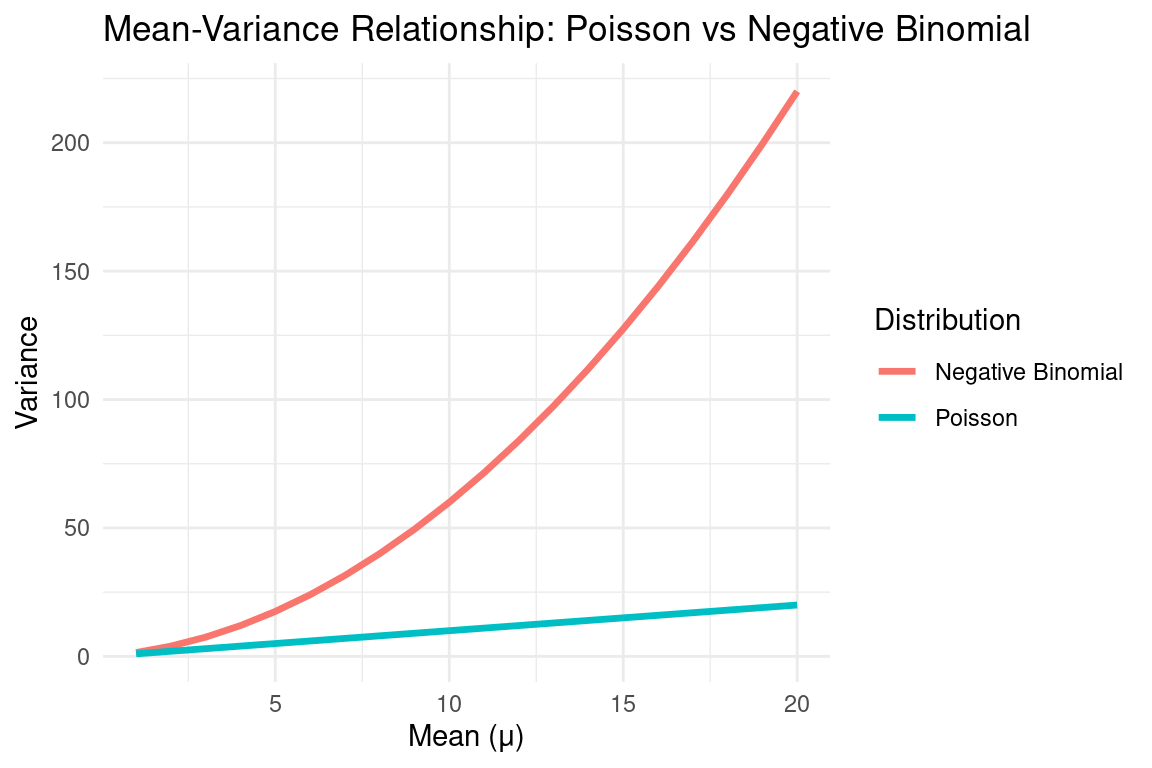
Example: Negative Binomial Distribution

  • A common solution for overdispersed count data.

  • Extends the Poisson distribution by introducing a dispersion parameter \(\alpha\):
    \[ \mathbb{E}(Y) = \mu, \quad \text{Var}(Y) = \mu + \alpha \mu^2. \]

  • When \(\alpha = 0\), it reduces to Poisson.

  • Random Effects Interpretation:

    • The Negative Binomial can be interpreted as a Gamma-Poisson mixture.
    • The Poisson mean \(\mu\) is drawn from a Gamma distribution, introducing extra variability.

Random Effects Models for Overdispersion

  • Overdispersion often arises due to unobserved heterogeneity.
  • A solution is to introduce random effects that account for latent variability.

. . .

  • Random Intercept Model:
    \[ Y_{ij} \mid Z_i \sim \text{Binomial}(p_{ij}), \quad \log\left\{\frac{p_{ij}}{1-p_{ij}}\right\} = \beta_0 + d_{ij} \beta_1 + Z_i. \]

. . .

  • \(Z_i \sim \mathcal{N}(0, \sigma^2)\) captures between-group variability.

. . .

  • Leads to extra variability in counts, addressing overdispersion.

. . .

  • Connection to Negative Binomial:
    • If \(Z_i\) follows a Gamma distribution instead of Normal, the model is equivalent to a Negative Binomial.

A class of generalized linear models

Assumptions:

. . .

  1. \(Z_{i}\) are i.i.d. random variables;

. . .

  1. \(Y_{i} \mid Z_i \sim f(\cdot)\) belongs to the exponential family;

. . .

  1. \(E[Y_{i}\mid Z_i] = m_i \mu_{i}\) and \(\text{Var}[Y_{i} \mid Z_i] = m_i V(\mu_{i})\);

. . .

  1. \(g(\mu_{i}) = \eta_i = d_i^\top \beta + Z_i\);

. . .

  1. \(Y_i \mid Z_i\) are mutually independent for \(i=1,\dots,n\).

Parameter Estimation

  • Let the \(Z_i\) be i.i.d. Gaussian distributions with mean zero and variance \(\sigma^2\).

  • Likelihood function

The vector of unkown parameters is \(\theta=(\beta, \sigma^2)\)

\[ L(\theta) = \prod_{i=1}^n \int_{-\infty}^{+\infty} [Z_i] [Y_i \mid Z_i] \: dY_i \]

. . .

  • Estimation Method

Maximize the likelihood using the Laplace approximation (glmer in the lme4 package).

. . .

  • Hypothesis Testing

    1. Obtain \(\hat{\theta}\) (MLE).
    2. Obtain \(\hat{\theta}_{0}\), the MLE constrained by fixing \(p\) values of \(\beta\) to 0.
    3. Compute the log-likelihood ratio:

    \[ D = 2(\log L(\hat{\theta}) - \log L(\hat{\theta}_0)) \sim \chi^2_{p} \]

    1. P-value: \(P(D > D_{obs} \mid H_0)\)

. . .

glmer_fit.R

Which residuals should we use to assess spatial correlation?

  • Pearson Residuals: \[\frac{y_i - \hat{y}_i}{\sqrt{\text{Var}(\hat{y}_i)}}\]

  • Deviance Residuals: \[\text{sign}(y_i - \hat{y}_i) \times \sqrt{d_i}\] where \(d_i\) is the deviance contribution of observation \(i\).

  • Random Effects Residuals: \(\hat{Z}_i\), i.e. the estimated random effect for each location/household/cluster/village.

The Empirical Variogram using Random Effects Residuals

  • The empirical variogram is defined as: \[ \gamma(D_{[a,b]}) = \frac{1}{2|D_{[a,b]}|} \sum_{(i,j) \in D_{[a,b]}} (\hat{Z}_i - \hat{Z}_j)^2 \] where:
    • \(D_{[a,b]}\) is a class of distance with lower limit \(a\) and upper limit \(b\);
    • \(|D_{[a,b]}|\) is the number of pairs of observations whose locations ar at a distance between \(a\) and \(b\).

. . .

. . .

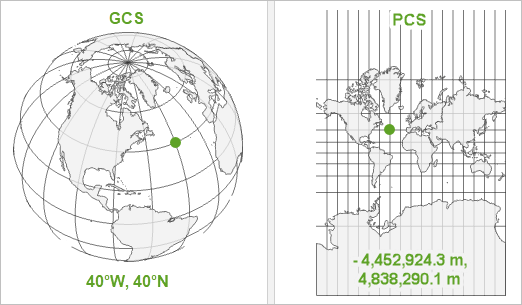
Coordinate Reference Systems (CRS)

Geographic vs. Projected CRS
  • A CRS tells us how the coordinates in our data match real-world locations on the Earth.
  • Two main types:
    • Geographic CRS (Latitude/Longitude, e.g., WGS84)
    • Projected CRS (e.g., UTM, which uses meters for measurements)

Computing Distance

  • Distances in Geographic CRS (Lat/Lon) require geodesic calculations (e.g., Haversine formula).

  • Projecting to UTM allows for Euclidean distance calculations in meters.

  • Conversion to UTM in R:

    library(sf)
points <- st_as_sf(data.frame(lon = c(-0.1, -0.2), lat = c(51.5, 51.6)), 
                   coords = c("lon", "lat"), crs = 4326)
points_utm <- st_transform(points, crs = 32630)

Spatial Data Formats

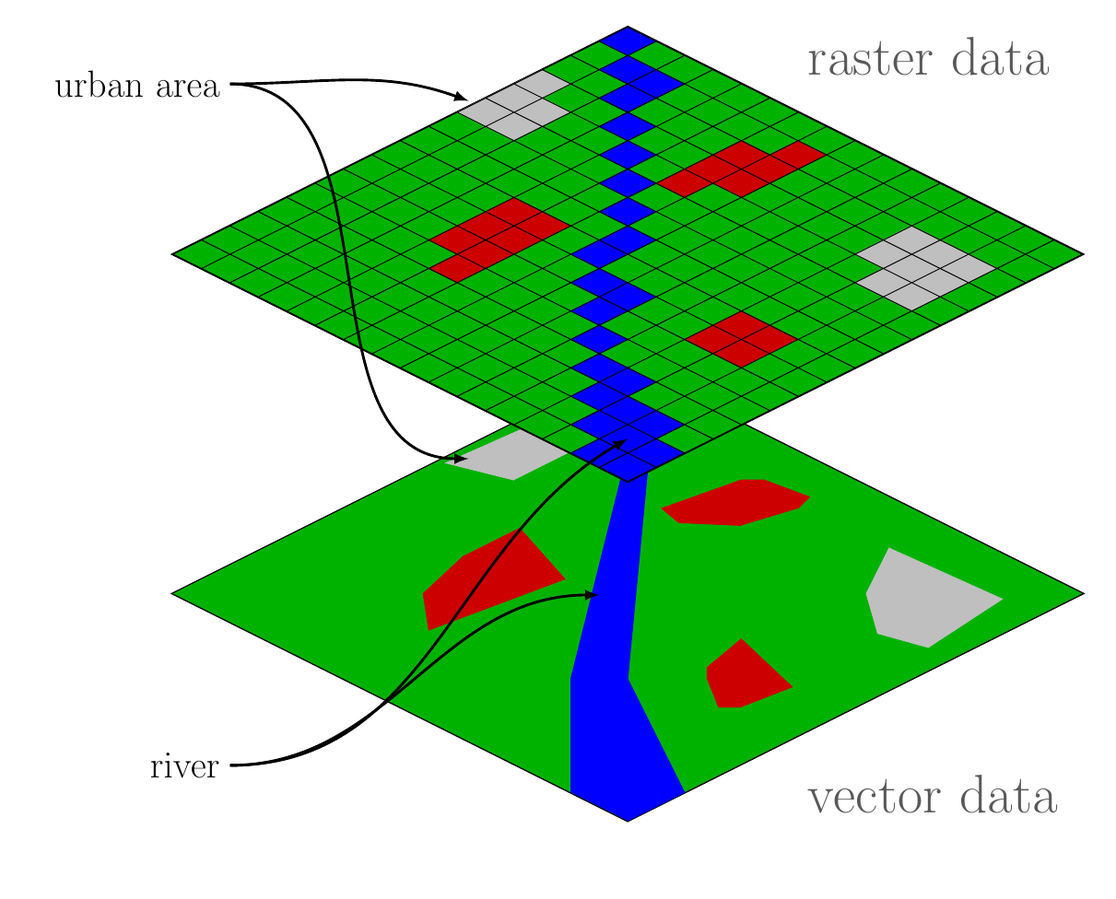
  • Shapefiles:
    • Vector data format for storing geometries (points, lines, polygons).
    • Commonly used in GIS applications.
  • Raster Files:

    • Grid-based data (e.g., satellite images, elevation models).

    • Each cell has a value representing an attribute (e.g., temperature, elevation).