Introduction

Model-based Geostatistics for Global Public Health

Author
Affiliation

Emanuele Giorgi

Lancaster University

Overview

  • Defining geostatistical problems
  • Model-based geostatistics as a data-driven approach to spatial analysis of health outcomes

Epidemiological Data

  • Incidence: Number of new cases per unit time per unit population
  • Prevalence: Number of existing cases per unit population
  • Risk: Probability that a person will contract the disease (per unit time or lifetime)

Objective: Understand spatial variation in disease incidence, prevalence, and risk

Relevant books:
Elliott et al. (2000), Gelfand et al. (2010), Rothman (1986), Waller & Gotway (2004), Woodward (1999)

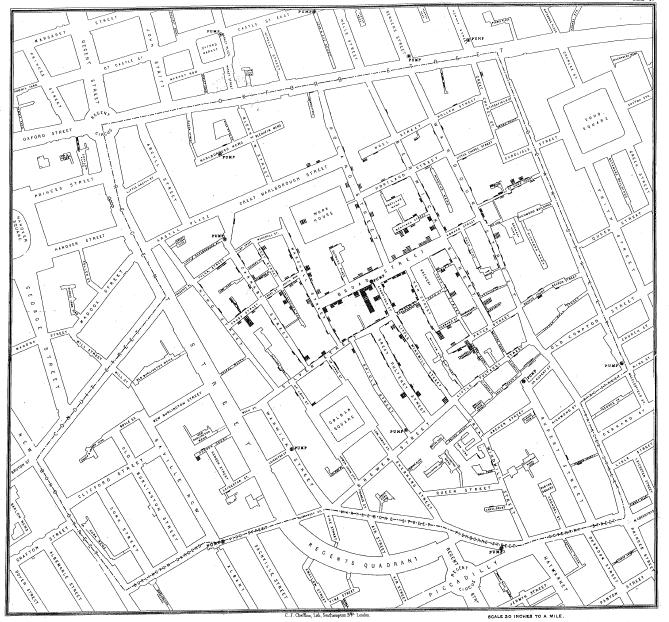
Cholera in Victorian London, 1854

  • John Snow removed the handle of the Broad Street water pump
  • Identified contaminated water as the disease source
  • Contradicted conventional wisdom at the time

1854 Broad Street cholera outbreak


Study Designs

  1. Registry
    • Case counts in sub-regions
    • Population size as denominator
    • Covariates from census data
  2. Case-Control
    • Cases: All known cases in the study region
    • Controls: Probability sample of non-cases
  3. Survey
    • Sampled locations within study region
    • Data collected per location
    • Common in low-resource settings

Registry Example: Plague in Madagascar

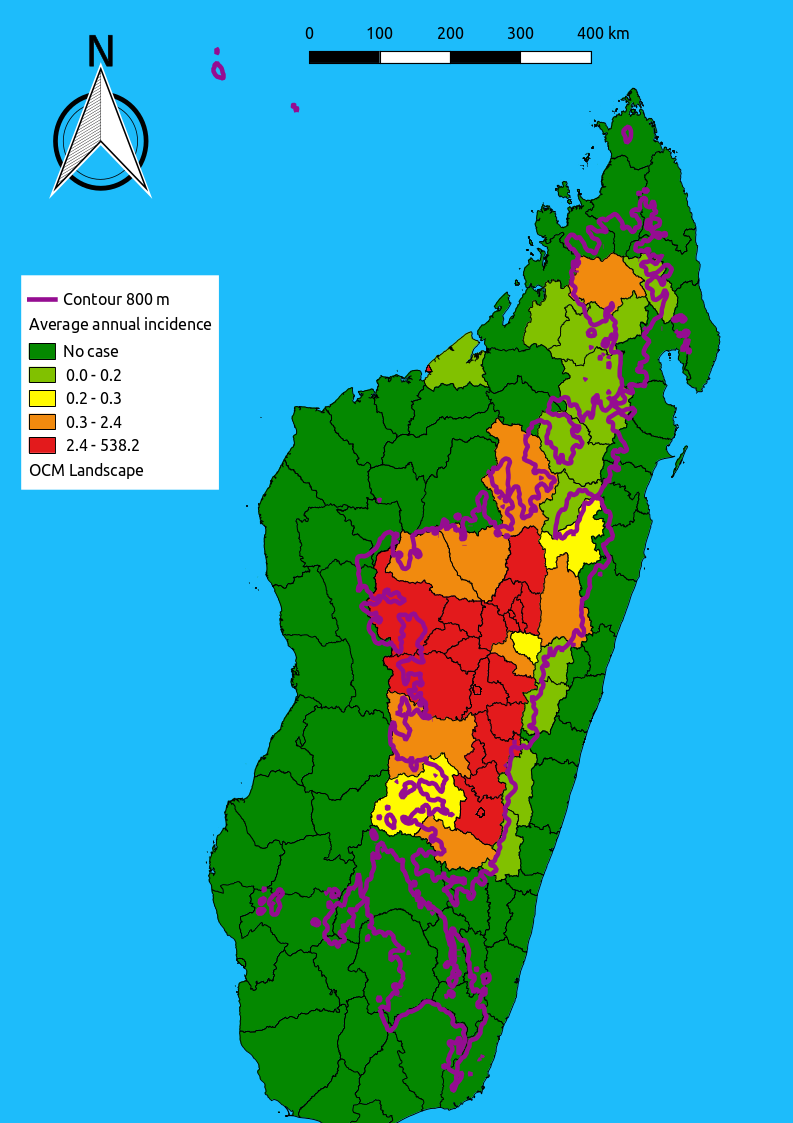
Research Question:
Does plague infection risk increase above 800m elevation?

Giorgi et al., 2016, Spatial and Spatio-temporal Epidemiology

Case-Control Example: Childhood Leukaemia in Humberside

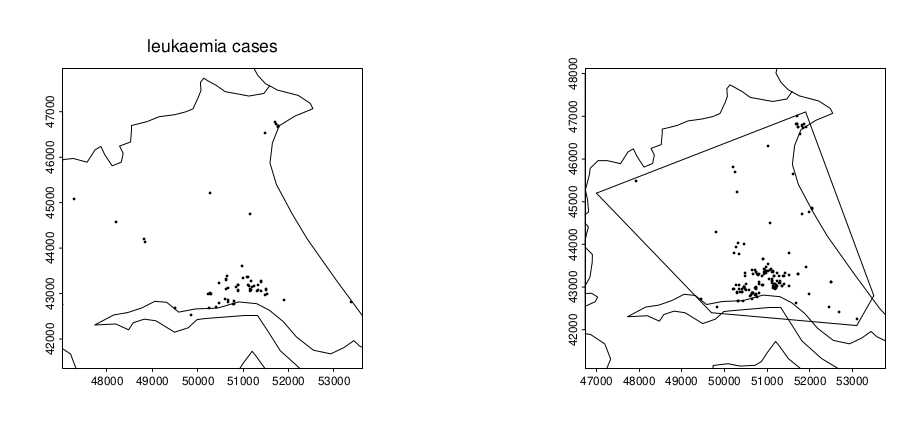
  • Locations of all known cases (1974–82)
  • Residential locations of a random sample of births

References:
Cuzick & Edwards (1990), Diggle & Chetwynd (1991)

Survey Example: Loa loa in Cameroon

  • Data: Empirical prevalences in surveyed villages
  • Map: Predictive probabilities of exceeding 20% prevalence threshold

Diggle et al., 2007

Research Questions

Plague in Madagascar

  • Is elevation an important risk factor?
  • If so, why?

Childhood Leukaemia in Humberside

  • Do cases show unexpected clustering?

Loa loa in Cameroon

  • What environmental factors influence risk?
  • Can we predict areas exceeding an intervention threshold?

Epidemic vs Endemic Patterns

  • Epidemic: Foot-and-mouth in Cumbria (2001)
  • Endemic: Gastroenteric disease in Hampshire (AEGISS)

Animations:
- Foot-and-mouth
- AEGISS

How are these patterns different?

Empirical Modelling: AEGISS Project

  • Objective: Early detection of incidence anomalies
  • 3,374 reports of gastro-intestinal illness
  • Log-Gaussian Cox process for space-time correlation

Geostatistics

  • Data: \((y_i, x_i)\), where \(x_i \in A \subset \mathbb{R}^2\)

  • Model: \(Y_i = S(x_i) + Z_i\)

  • Objective: Estimate \(\int_{A} S(x) dx\) (e.g., mining yield)

Model-Based Geostatistics for Public Health


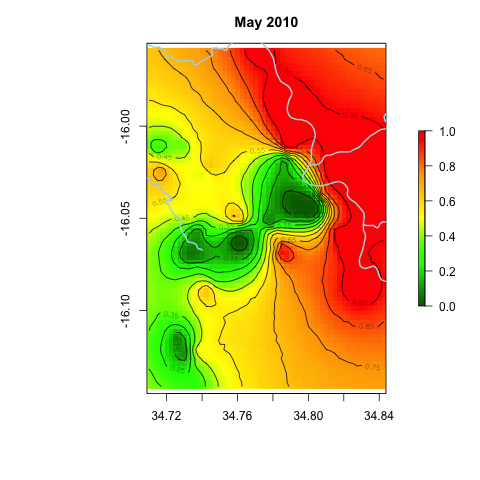
Animation: Malaria in Chikwawa district

Science and Statistics

Key Concepts:
- \(S\): “Process of nature”
- \(Y\): “Observed data”
- Bayesian Framework: \([Y, S] = [S][Y | S]\)

Adapted from: Statistics and Scientific Method (Diggle & Chatwynd, 2011)

Workflow of a statistical analysis

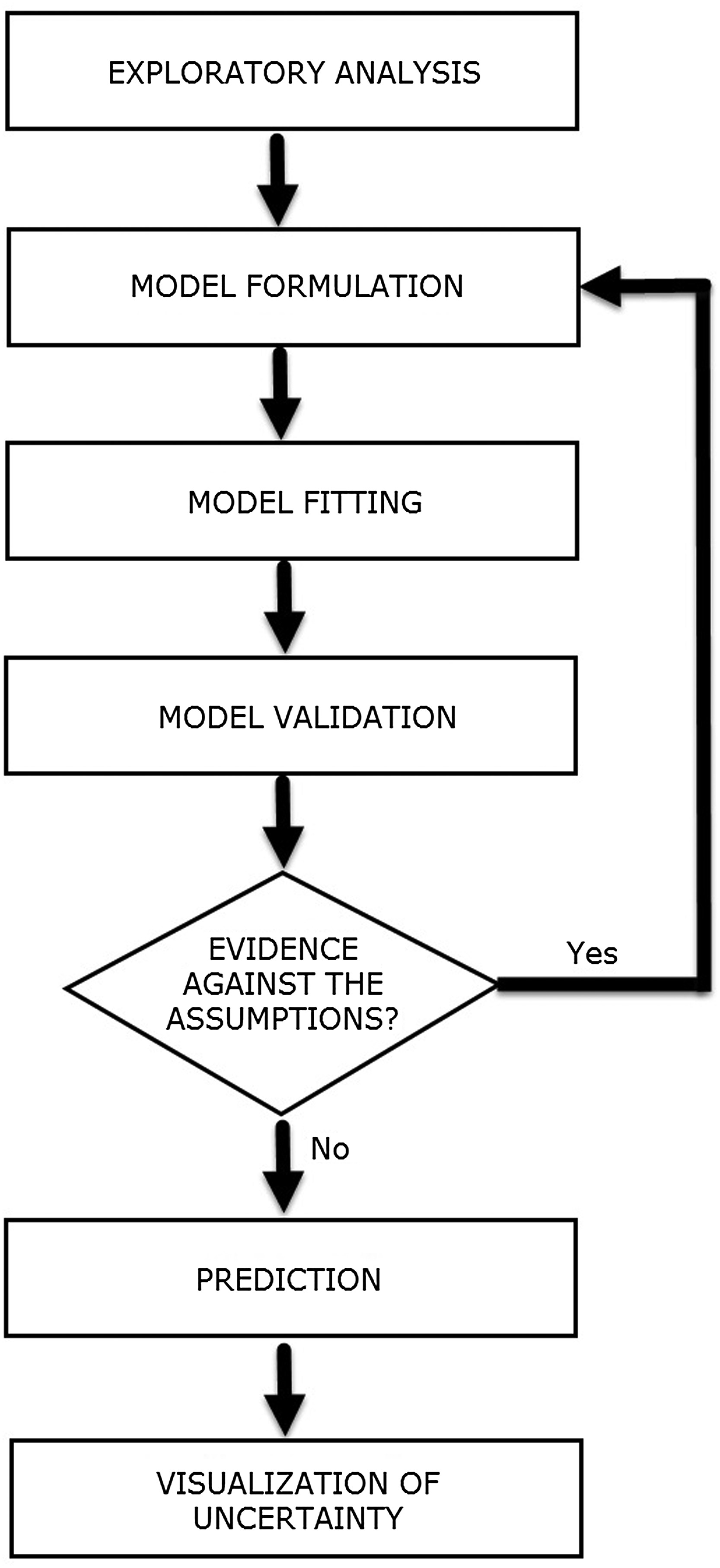
How do we apply the workflow of a statistical analysis in model-based geostatistics?